Written on 2012年1月17日 @ 12:22 | by sc | Tags: 旋转矩阵
但是,没关系用这种手腕爆发旋转矩阵,然后哄骗其他的优化算法对它再进一步优化,这样没关系爆发对照精良的旋转矩阵。
4.诱致算法。Greg Kuperdevelop intorg是这种算法的严重建树者和倡始者。
先哄骗一个庞大的参数为(VKt) 的旋转矩阵 ,从V个点中依照某种次序或完全随机的选出v个点,然后将他们用正本的长度为 K的区组隔断,取得了每个区组个数不定的一个笼盖。末了,将这个笼盖实行如下的修补即可:对每一个长度为l的区组,将该区组替代成一个(lkt)的笼盖计划。这是一种对照纷乱的算法,不过,确是迄今最好的算法之一。
运用他没关系爆发优化水平对照高的矩阵。不过,运用这种算法的一个很大的限制是,必必要有一个参数很大的旋转矩阵和许许多多的参数比它小的矩阵。
四、旋转矩阵的算法
1.模仿退火Simulgotd Anneasing算法
模仿冷却算法是一种随机搜寻手腕,它的严重特质是不消穷遍鸠集中每一种可能性就没关系找到最优或简直最优的形态。它是经历模仿一个分子体例的天然冷却体例来做到这一点的。在每一种形态,它随机地拔取了一种相邻的形态,如这种相邻的形态有一个更低的本钱,体例将会转移到该形态。假如这种相邻的形态有一个更高的本钱,体例将可能会转移到该形态,也可能不会转移到该形态。转移的概率依赖于此刻的形态的温度参数(该值越高,转移的概率越大)和两个形态之间的本钱的不同(不同越大,转移的概率越大)。温度将会垂垂低上去,最终会抵达平衡。模仿冷却算法不时用来尝试挖掘割裂数学中一些题目的简直最优的解。
2.非连通的鸠集算法来结合笼盖计划
假如对某个v=v1+v2和全盘的t1+t2=t都有大小为N1的笼盖计划(v1k1t1)和大小为N2的笼盖计划(v2k2t2)保存,听听双色球预测软件。那么将有大小为N=N1*N2的笼盖计划保存。不过,没关系用这种手腕爆发的旋转矩阵数量很少,而且组织的历程也很纷乱。很少的旋转矩阵是用这种手腕爆发的。
3.贪心算法。这种算法爆发了许多许多的旋转矩阵。这种算法的重点思想是:每个区组都尽可能少反复后面区组的数字,平昔反复上去,
初始化 却无法保证产生的旋转矩阵一定是最优的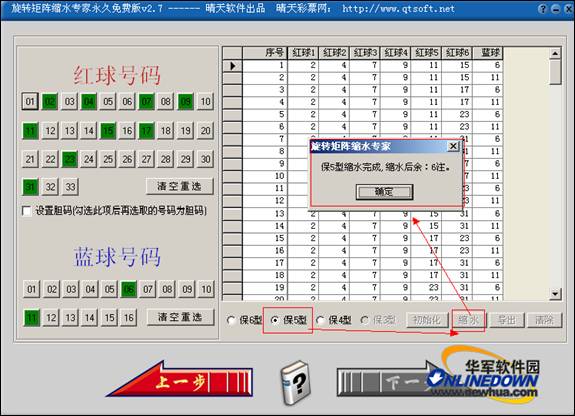
直到你取得一个笼盖计划。你没关系用次序、逆序或灰色、随机的次序来反复这个历程。大概没关系用你所嗜好的计划。底细上,笔者开初的时间正是用这个手腕来爆发一些对照简易的矩阵,但是这种算法看起来容易,现实上却极度烦琐,假如不消计算机,纵然是很简易的矩阵,也要消耗有数的元气?心灵。而且,这种算法只能保证没关系爆发旋转矩阵,却无法保证爆发的旋转矩阵必然是最优的。当参数很大时,用它爆发的矩阵离最优的矩阵还差的很远。双色球2。
但是,没关系用这种手腕爆发旋转矩阵,然后哄骗其他的优化算法对它再进一步优化,这样没关系爆发对照精良的旋转矩阵。
4.诱致算法。Greg Kuperdevelop intorg是这种算法的严重建树者和倡始者。
先哄骗一个庞大的参数为(VKt) 的旋转矩阵 ,从V个点中依照某种次序或完全随机的选出v个点,然后将他们用正本的长度为 K的区组隔断,取得了每个区组个数不定的一个笼盖。末了,将这个笼盖实行如下的修补即可:对每一个长度为l的区组,将该区组替代成一个(lkt)的笼盖计划。这是一种对照纷乱的算法,不过,确是迄今最好的算法之一。
运用他没关系爆发优化水平对照高的矩阵。不过,运用这种算法的一个很大的限制是,必必要有一个参数很大的旋转矩阵和许许多多的参数比它小的矩阵。
0 Response to “却无法保证产生的旋转矩阵一定是最优的”